WHAT
IS
LARGE
SCALE
STRUCTURE
?
As we look out into the universe we see structure on a wide range of
physical scales. The most obvious example is that stars cluster in
groups and galaxies.
Early redshift surveys of the 1980s showed that these galaxies are also
not distributed randomly throughout the Universe. They are found to lie in
clusters, filaments, bubbles and sheet
like structures.
There exist large regions of the Universe which contain almost no galaxies.
The nearby universe then shows a large amount of structure on the very
largest scales.
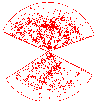 The positions of galaxies in the Center for Astrophysics (CfA) redshift
survey. The plot shows a thin slice through the universe (the pie shapes)
containing nearly 10,000 galaxies.
The observer is situated at the narrow end of the slice. Distances radially
outward indicate the observed redshift of a galaxy.
The positions of galaxies in the Center for Astrophysics (CfA) redshift
survey. The plot shows a thin slice through the universe (the pie shapes)
containing nearly 10,000 galaxies.
The observer is situated at the narrow end of the slice. Distances radially
outward indicate the observed redshift of a galaxy.
Recent very large scale galaxy surveys
have now reached far enough out into our local volume to begin to see
the end of greatness. That is they sample a large enough volume
of space that the largest structures in the survey (about 100Mpc in size)
are no longer of the same size of the survey itself.
Galaxy surveys with well defined selection criteria enable us to extract
information about the clustering pattern. Such surveys are driven in part
by the map-makers instinct: the desire to discover and name the structures
which we can see through our telescopes. They are also driven by a more
theoretical desire: they provide the data with which we can test our ideas
about the origin of structure in the universe.
To characterize the distribution of galaxies a number of statistical tools
have been developed. The most widely used approach to quantifying the degree
of clustering observed is to measure the correlation functions. For example
the two-point correlation function is the probability, in excess of random,
of finding a galaxy at a fixed distance from a random neighbor.
Its Fourier transform is the power spectrum (which is now more widely used).
Beyond this one investigates higher order correlation functions, for example
the distribution of counts-in-cells: the distribution of the number of
galaxies found in cells of a given size which one lays down atop the survey.
For further information go here.
Return to my research interests page for a
bibliography.
 Back to Home Page
Back to Home Page
Back to
Site Index
 The positions of galaxies in the Center for Astrophysics (CfA) redshift
survey. The plot shows a thin slice through the universe (the pie shapes)
containing nearly 10,000 galaxies.
The observer is situated at the narrow end of the slice. Distances radially
outward indicate the observed redshift of a galaxy.
The positions of galaxies in the Center for Astrophysics (CfA) redshift
survey. The plot shows a thin slice through the universe (the pie shapes)
containing nearly 10,000 galaxies.
The observer is situated at the narrow end of the slice. Distances radially
outward indicate the observed redshift of a galaxy.
